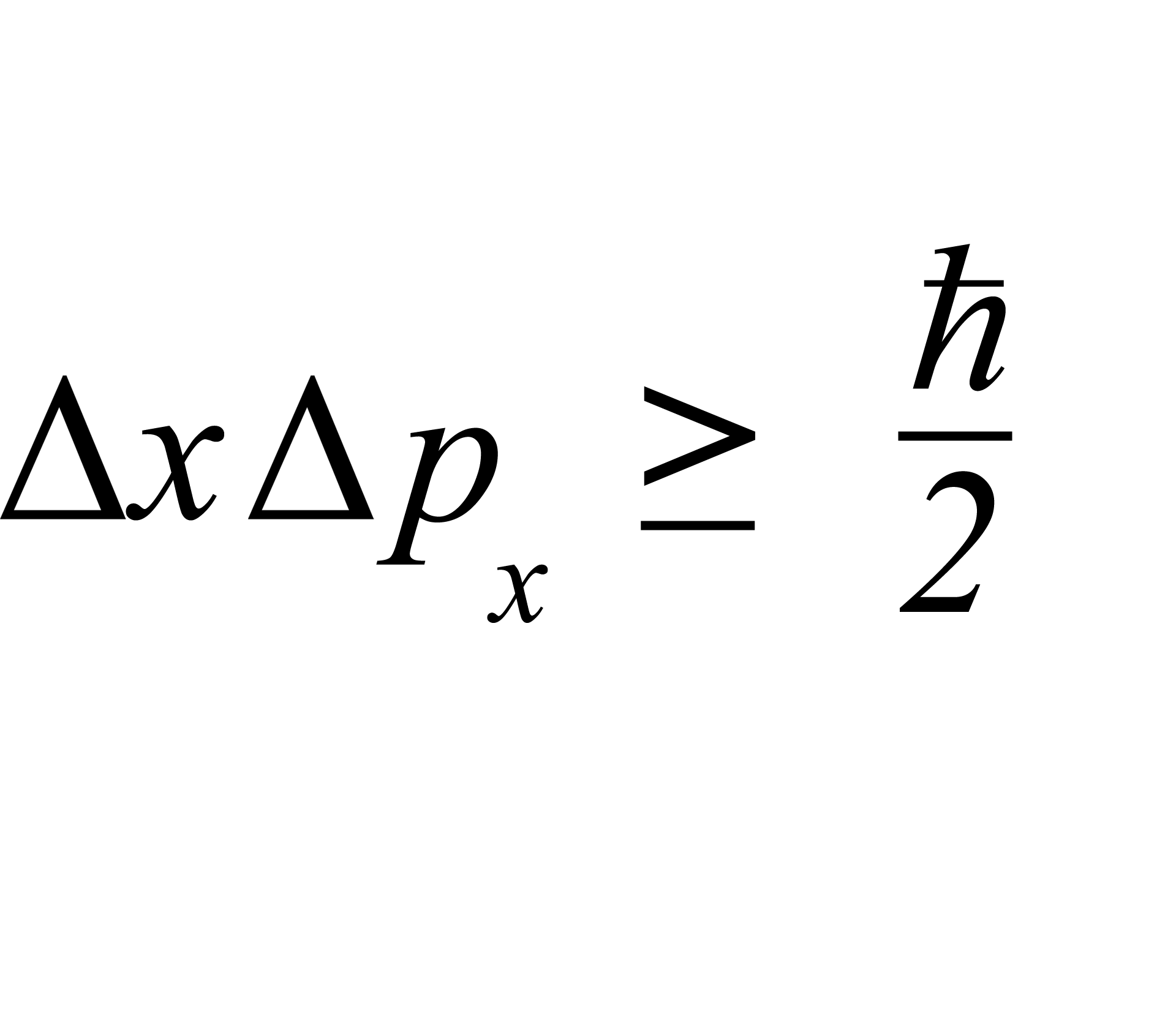Die Heisenbergsche Unschärferelation oder Unbestimmtheitsrelation (seltener auch Unschärfeprinzip) ist die Aussage der Quantenphysik, dass zwei komplementäre Eigenschaften eines Teilchens nicht gleichzeitig beliebig genau bestimmbar sind. Das bekannteste Beispiel für ein Paar solcher Eigenschaften sind Ort und Impuls.
Die Unschärferelation ist nicht die Folge technisch behebbarer Unzulänglichkeiten eines entsprechenden Messinstrumentes, sondern prinzipieller Natur. Sie wurde 1927 von Werner Heisenberg im Rahmen der Quantenmechanik formuliert. Die heisenbergsche Unschärferelation kann als Ausdruck des Wellencharakters der Materie betrachtet werden. Sie gilt als Grundlage der Kopenhagener Deutung der Quantenmechanik.[1][2]
Quantenmechanik und klassische Physik
Die Quantenmechanik ist eine der fundamentalen Theorien für die Beschreibung unserer physikalischen Welt. Der konzeptionelle Aufbau dieser Theorie unterscheidet sich tiefgreifend von dem der klassischen Physik.
Die Aussagen der Quantenmechanik über unsere Welt sind Aussagen über Ausgänge von Messungen. Im Gegensatz zur klassischen Physik können in jedem Fall nur Wahrscheinlichkeitsaussagen getroffen werden, man kann also nur die Werteverteilung bei der Messung an einem Ensemble von gleichartigen Systemen vorhersagen. Die heisenbergsche Unschärferelation ergibt sich daraus, dass ein physikalisches System in der Quantenmechanik mit Hilfe einer Wellenfunktion beschrieben wird. Während in der klassischen Mechanik Ort bzw. Impuls einfache Größen sind, die prinzipiell exakt messbar sind, ergeben sich ihre Verteilungen in der Quantenmechanik als Betragsquadrat der Wellenfunktion bzw. ihrer Fouriertransformierten, d. h., sie sind nicht unabhängig voneinander festlegbar. Da die Verteilungen von Ort und Impuls beide von der Wellenfunktion des Systems abhängen, sind auch die Standardabweichungen der Messungen voneinander abhängig. Je genauer man den Ort eines Teilchens in der üblichen quantenmechanischen Beschreibung festlegen will, umso größer wird die Unschärfe des Impulses – und umgekehrt.
Folgende Analogie veranschaulicht die Unbestimmtheit: nehmen wir an, dass wir ein zeitveränderliches Signal haben, z. B. eine Schallwelle, und wir die genaue Frequenz dieses Signals zu einem bestimmten Zeitpunkt messen wollen. Das ist unmöglich, denn um die Frequenz einigermaßen exakt zu ermitteln, müssen wir das Signal über eine genügend lange Zeitspanne beobachten (siehe Küpfmüllersche Unbestimmtheitsrelation), und dadurch verlieren wir Zeitpräzision. D. h., ein Ton kann nicht innerhalb nur einer beliebig kurzen Zeitspanne da sein, wie etwa ein kurzer Schrei, und gleichzeitig eine exakte Frequenz besitzen, wie sie etwa ein ununterbrochener reiner Ton hat. Die Dauer und die Frequenz der Welle sind analog zum Ort und Impuls eines Teilchens zu betrachten.
Ursprüngliche Formulierung
Die erste Formulierung einer Unschärferelation in der Quantenmechanik betraf die gleichzeitige Kenntnis von Ort und Impuls eines Teilchens. Im Jahre 1927 veröffentlichte Heisenberg seine Arbeit über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik[1] und argumentierte, dass die mikroskopische Bestimmung des Ortes 

Einerseits ist die Ungenauigkeit 




Der zunächst qualitative Charakter dieser Abschätzung rührt daher, dass die Aussage nicht (streng) bewiesen und die verwendete Notation für die Unbestimmtheiten nicht genau definiert ist. Bei geeigneter Interpretation der Notation im Rahmen der modernen Quantenmechanik zeigt sich jedoch, dass die Formel der Realität sehr nahekommt.
Unschärferelation und Alltagserfahrung
Warum diese charakteristischen Unbestimmtheiten weder im Alltag noch in der Forschung früher bemerkt worden waren, kann man verstehen, wenn man sich die Kleinheit des Planckschen Wirkungsquantums gegenüber den typisch erreichbaren Messgenauigkeiten für Ort und Impuls vergegenwärtigt. Dazu die folgenden Beispiele:
Radarkontrolle im Straßenverkehr
Der Ort des Fahrzeugs sei bei der Radarkontrolle bis auf 





Staubkorn
Bei einem extrem genau mikroskopierten Staubkorn von einer Masse 



Elektron im Atom
Ein Atom hat einen Durchmesser von etwa einem Ångström. Bei einer kinetischen Energie eines darin gebundenen Elektrons von etwa 





Aussagen
Unter dem Begriff des Unschärfe- oder auch Unbestimmtheitsprinzips werden die folgenden Aussagen zusammengefasst, die zwar miteinander verwandt sind, jedoch physikalisch unterschiedliche Bedeutung haben.[4] Sie sind hier beispielhaft für das Paar Ort und Impuls notiert.
- Es ist nicht möglich, einen quantenmechanischen Zustand zu präparieren, bei dem der Ort und der Impuls beliebig genau definiert sind.
- Es ist prinzipiell unmöglich, den Ort und den Impuls eines Teilchens gleichzeitig beliebig genau zu messen.
- Die Messung des Impulses eines Teilchens ist zwangsläufig mit einer Störung seines Ortes verbunden, und umgekehrt.
Jede dieser drei Aussagen lässt sich quantitativ in Form sogenannter Unschärferelationen formulieren, die eine untere Grenze für die erreichbare minimale Unschärfe der Präparation bzw. Messung angeben.
Auch zwischen anderen Paaren physikalischer Größen können Unschärferelationen gelten. Die Voraussetzung dafür ist, dass der Kommutator der beiden den Größen zugeordneten quantenmechanischen Operatoren nicht null ist. Beispielsweise haben Franke-Arnold u. M. experimentell nachgewiesen, dass eine entsprechende Relation zwischen Winkelstellung und Drehimpuls gilt.[5]